数学到底有多重要

数学不仅可以科学研究，也可以让普通人了解生活中常见问题的原因。 在此，列举两个与天气预报和医疗诊断这一数学无关的例子。 通过数学分析可以看出，天气误报、医院误诊不能完全怪气象台和医院，有时是数学问题。 天气预报

1、数学的实践与认识外文文献，数学到底有多重要？

天气预报很多人说，现在科学这么发达，为什么天气预报不好？ 这里涉及一个叫做条件概率的数学问题。

什么是条件概率呢？

例如，确认6月15日是否下雨。 根据往年的经验，下雨的概率是40%，不下雨的概率是60%，这叫做概率。 前一天，天气预报说6月15日下雨的情况，我们把这个叫做条件，在这个条件下6月15日真的下雨的概率叫做条件概率。

天气预报根据一定的气象参数决定是否有可能下雨，由于天气不太清楚，即使预报下雨也有可能是晴天。 假设天气预报准确率为90%，下雨的情况下，预报有90%的概率下雨，预报有10%的概率不下雨； 同样在不下雨的情况下，预报有10%的概率下雨，预报有90%的概率不下雨。

于是，6月15日的预报和天气有四种可能性，要么预报下雨真的下雨，要么预报不下雨但下雨，要么天气预报预报下雨不下雨，要么预报不下雨真的不下雨。 下表显示了四种情况，并计算每个情况的概率。

计算方法是两个概率的乘积。 例如下雨的概率是40%，预报下雨的概率是90%，所以如果预报下雨下雨，占4种情况的概率是36%。 同样，天气预报可以计算出下雨但不下雨的概率为6%，两者之和为42%，这就是天气预报下雨的概率。

这42%的可能性中，真的下雨的可能性是36%，比例是

不下雨的概率是6%

也就是说，在天气预报准确率为90%的情况下，预报有雨，真正下雨的概率只有85.7%。 可见，预报下雨时是否真的下雨，不仅与预报的精度有关，还与这个地区平时下雨的概率有关。

医疗检查与这个问题相似的是，在医院进行重大疾病检查时，如果医生发现异常，一般不直接断定是病，而是建议去大医院再检查一次。 虽然这两次检查可能完全一样。 为什么会这样呢？

假设存在某种重大疾病，患病人群占全组的比例为1/7000。 也就是说，立即选人，有1/7000的概率患此病，有6999/7000的概率不患此病。

有先进的检查方法，误诊率只有万分之一。 也就是说，患病人群有1/10000的可能性被误诊为健康人，健康人也有1/10000的可能性被误诊为患病。

我们必须问。 在一次检查得到生病结果的前提下，那个人真正生病的概率是多少？

我们效仿刚才的做法，检测出患病的总概率

患病且检出患病的概率是

所以，如果检测到疾病，真正生病的概率如下。

显而易见，即使是万分之一的误诊，一次检查也不能完全确定一个人是否生病。

那么，两次检查都有患病，情况如何？

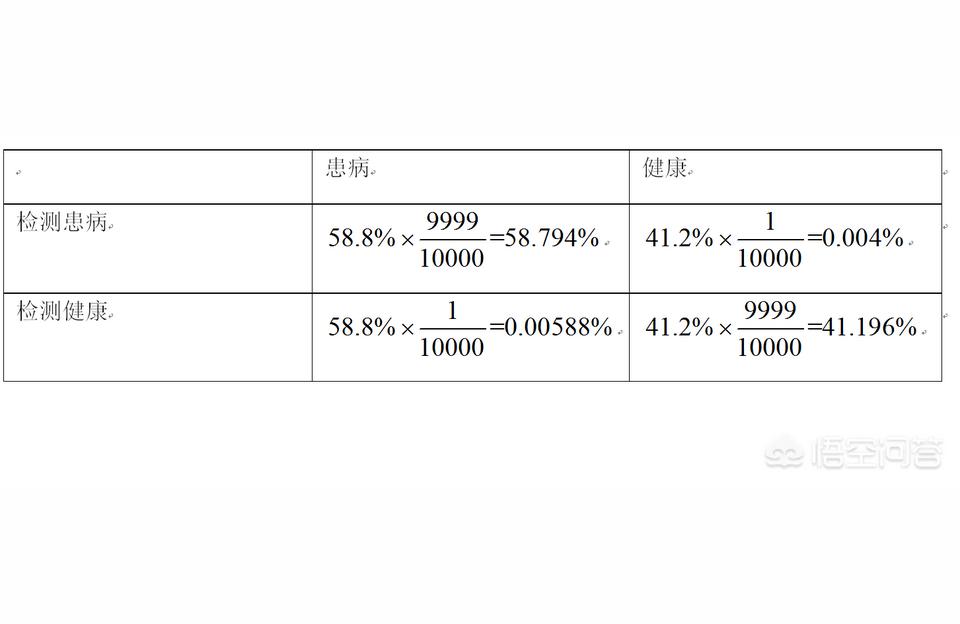
请注意，在第一次检查结果生病的前提下，这个人生病的概率已经不是所有人的1/7000，而是自己的58.8%，健康的概率只有41.2%，所以第二次检查的表格是：

如果两次检查都患病，此人真正患病的概率如下。

我几乎没跑。

详细讨论这个问题的人是英国数学家贝思。

贝叶斯表示，如果a和b是两个相关事件。 a有可能发生，也有可能不发生，b有B1、B2、…、Bn的合计n种可能性。 那么，以发生a为前提发生Bi的概率称为条件概率P(Bi|A )。

为了计算这个概率，首先计算在Bi发生的条件下a发生的概率。 公式为p(bi ) p ) a|bi。

然后，需要通过将每个Bi事例中发生的概率与该事例中发生a的概率相乘，再加上乘积来计算事件a发生的总概率。

最后，除以上述两个概率。 完整的贝叶斯公式如下

贝叶斯公式在社会学、统计学、医学等领域起着很大的作用。

1-@ .comshuminghao 123 Shuming hao123 Shuming hao123 Shuming hao123 Shuming hao123 Shuming hao123 Shuming hao123 3 Shuming hao123 Shuming hao123 Shuming hao123 Shuming hao123 Shuming hao123 Shuming hao123 Shuming hao123 Shuming hao123 ing hao123 Shuming hao123 Shuming hao123 Shuming hao123 Shuming hao123 Shuming hao123 Shuming hao123 Shuming hao123 Haoo 123 Shuming Haoo 123 Shuming Haoo 123 Shuming Haoo 123 Shuming Haoo 123 Shuming Haoo 123 Shuming Haoo 123

文章来源：《数学的实践与认识》 网址: http://www.sxdsjyrs.cn/zonghexinwen/2022/1206/1068.html